Сумма двух катетов прямоугольного треугольника - это простая, но важная величина в геометрии. Рассмотрим ее свойства и значение в математических расчетах.
Содержание
Сумма двух катетов прямоугольного треугольника - это простая, но важная величина в геометрии. Рассмотрим ее свойства и значение в математических расчетах.
Основные понятия
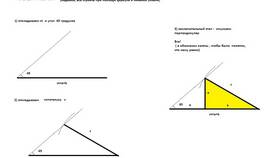
В прямоугольном треугольнике:
- Катеты - это две стороны, образующие прямой угол
- Гипотенуза - сторона, противоположная прямому углу
- Сумма катетов - это их арифметическое сложение (a + b)
Формулы и соотношения
| Элемент треугольника | Обозначение |
| Первый катет | a |
| Второй катет | b |
| Сумма катетов | a + b |
Связь с другими элементами треугольника
Сумма катетов связана с:
- Гипотенузой (c) через теорему Пифагора: c = √(a² + b²)
- Периметром треугольника: P = a + b + c
- Площадью треугольника: S = (a × b)/2
Практическое применение
- В строительстве для расчета материалов
- В навигации для определения расстояний
- В физике при решении задач о движении
- В компьютерной графике для расчетов координат
Пример расчета
Для треугольника с катетами 3 см и 4 см:
| Сумма катетов | 3 + 4 = 7 см |
| Гипотенуза | √(3² + 4²) = 5 см |
| Периметр | 3 + 4 + 5 = 12 см |
| Площадь | (3 × 4)/2 = 6 см² |
Интересные свойства
- Сумма катетов всегда больше гипотенузы (a + b > c)
- Отношение суммы катетов к гипотенузе зависит от углов треугольника
- В равнобедренном прямоугольном треугольнике a = b
Понимание суммы катетов важно для решения геометрических задач и имеет много практических применений в науке и технике.
